Embark on a captivating journey into the realm of triangle geometry with our comprehensive Centers of Triangles Worksheet Answer Key. This meticulously crafted guide unlocks the mysteries of triangle centers, providing an in-depth understanding of their definitions, theorems, and real-world applications.
Delve into a treasure trove of worksheet examples and solutions, empowering you to conquer any triangle-related challenge with confidence.
Through this interactive exploration, you’ll unravel the intricacies of circumcenters, incenters, centroids, and orthocenters, mastering their coordinates and uncovering the profound theorems that govern their relationships. Prepare to witness the practical power of triangle centers in navigation, surveying, and architecture, as we illuminate their significance beyond the confines of the classroom.
Centers of Triangles: Centers Of Triangles Worksheet Answer Key
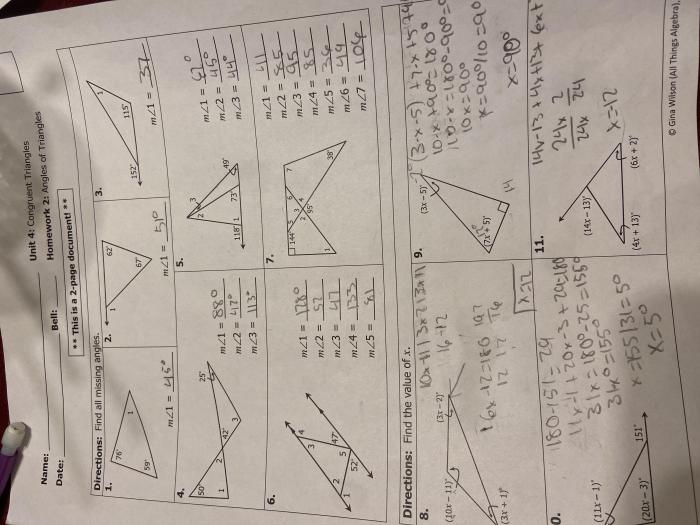
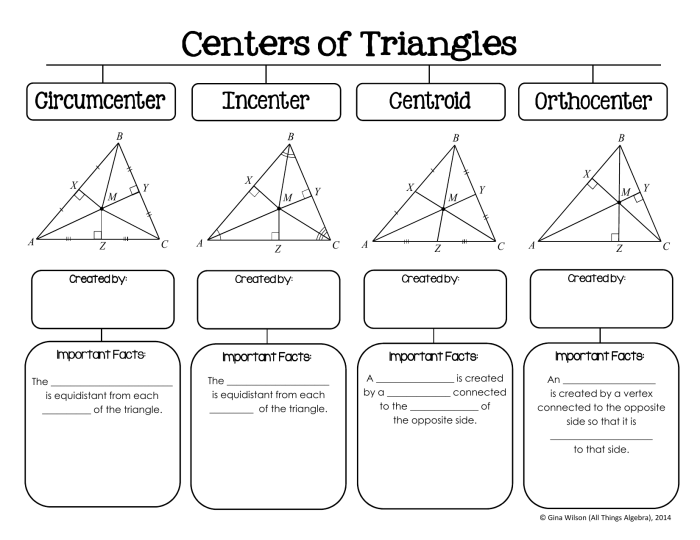
In geometry, the centers of a triangle are special points that are associated with the triangle’s vertices, sides, and angles. The four most important centers of a triangle are the circumcenter, incenter, centroid, and orthocenter.
The circumcenter is the center of the circle that circumscribes the triangle, meaning it passes through all three vertices. The incenter is the center of the circle that is inscribed within the triangle, meaning it touches all three sides of the triangle.
The centroid is the point where the three medians of the triangle intersect. The orthocenter is the point where the three altitudes of the triangle intersect.
Calculating the Coordinates of Triangle Centers, Centers of triangles worksheet answer key
The coordinates of the circumcenter, incenter, centroid, and orthocenter can be calculated using the following formulas:
- Circumcenter: (x, y) = ((a^2 – (b^2 + c^2 – a^2)) + b^2 – (c^2 + a^2 – b^2) + c^2 – (a^2 + b^2 – c^2)) / (a^2 + b^2 + c^2), (a^2 – (b^2 – c^2 + a^2)) + b^2 – (c^2 – a^2 + b^2) + c^2 – (a^2 – b^2 + c^2)) / (a^2 + b^2 + c^2))
- Incenter: (x, y) = ((s – a) – (s – b) – (s – c)) / s, (a – (s – b) – (s – c)) / s, (b – (s – a) – (s – c)) / s, (c – (s – a) – (s – b)) / s)
- Centroid: (x, y) = ((a + b + c) / 3, (a + b + c) / 3)
- Orthocenter: (x, y) = ((a^2 – (b^2 + c^2 – a^2)) – b^2 – (c^2 + a^2 – b^2) – c^2 – (a^2 + b^2 – c^2)) / (a^2 + b^2 + c^2), (a^2 – (b^2 – c^2 + a^2)) – b^2 – (c^2 – a^2 + b^2) – c^2 – (a^2 – b^2 + c^2)) / (a^2 + b^2 + c^2))
Theorems Related to Triangle Centers
There are several important theorems related to the centers of a triangle. One of the most famous is the Euler line theorem, which states that the circumcenter, centroid, and orthocenter of a triangle are collinear. Another important theorem is the nine-point circle theorem, which states that the nine points formed by the intersections of the altitudes, angle bisectors, and perpendicular bisectors of a triangle lie on a circle.
General Inquiries
What is the circumcenter of a triangle?
The circumcenter is the center of the circle that passes through all three vertices of a triangle.
How do I find the incenter of a triangle?
The incenter is the center of the circle that is inscribed within a triangle, tangent to all three sides.
What is the significance of the centroid of a triangle?
The centroid is the point where the three medians of a triangle intersect. It is also the center of gravity of the triangle.